Nabla ∇
- JC Duval

- 14 déc. 2025
- 2 min de lecture
Dernière mise à jour : 22 déc. 2025
Nabla est un opérateur vectoriel.
✧ Nabla est un être mathématique bivalent. C’est un vecteur mais c’est aussi un opérateur différentiel.

[∇] Associé à une fonction, Nabla désigne l'opérateur gradient.
Le gradient d'une fonction ayant plusieurs variables, est un champ de vecteurs qui combine les dérivées partielles de la fonction pour chacune de ses variables. En chaque point de la fonction, il donne la direction de la variation la plus élevée ainsi que son intensité.
L’opération en un point, donne un vecteur.
[∇.] Dans un produit scalaire, Nabla désigne l'opérateur divergence.
L'opération sur le vecteur donne un scalaire.
[∇^] Dans un produit vectoriel, Nabla désigne l'opérateur rotation.
L'opération sur le vecteur donne un vecteur.
Gradient
✧ On peut faire l’analogie avec un relief où la fonction f(M) s’apparente à l’altitude du point M ; l'ensemble des gradients de f(M) est un champ vectoriel, dont les lignes de champ sont analogues aux lignes de plus forte pente, orthogonales aux lignes constantes qui forment les courbes de niveau.
✧ ⛷ Si le déplacement est ⊥ au gradient, alors la pente du skieur est nulle, s'il est // alors elle est maximale.

Les vecteurs tangents à la ligne qui relie les points A et B, sont ⊥ aux courbes de niveau et leur longueur dépend de la pente.
Divergence
✧ La signification de l’opérateur divergence est liée à la notion de flux : un champ de vecteurs diverge (positivement ou négativement) en un point, si son flux à travers un volume élémentaire entourant ce point n’est pas nul.

Rotationnel
✧ Un champ de vecteurs dont le rotationnel est non nul en un point effectue une rotation autour de ce point. Le rotationnel renseigne sur le caractère tourbillonnaire du champ.


Nabla ∇
∇ = Nabla
Laplacien Δ
✧ Par construction, le Laplacien scalaire est la divergence du gradient du champ.

✧ Le rotationnel du rotationnel d'un champ est égal au gradient de la divergence de ce champ moins son Laplacien vectoriel.

Δ = Nabla²

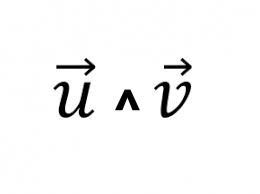


Commentaires